Modelling Intentionality: The Gambler

Rik Blok

A lecture for Physics 510: Stochastic Processes in Physics, by Birger Bergersen.

Introduction

$\bullet\;$ We have considered many models with autonomous individuals or agents (eg. birth/death, citizens of cities, ants).

$\bullet\;$ Agents have been modelled by assuming simple probability distribution for possible actions and treating as unmotivated, ``dumb'' particles (eg. birth/death rate, diffusion).

$\bullet\;$ Advantage: allowed analytical solutions via Master or Fokker-Planck equations.

$\bullet\;$ Disadvantage: often not very realistic.

$\bullet\;$ Introducing intentional motivated agents can complicate analysis but can be very rewarding [1,2,3].

$\bullet\;$ Simplest to make agents perfectly rational with complete knowledge and unlimited computational ability.

$\bullet\;$ Tends to produce simple, static equilibria (eg. ants make a bee-line straight for food).

$\bullet\;$ Aside: selfish motives can produce sub-optimal behaviour (eg. Braes' paradox [4], Diner's Dilemma [5])

Bounded Rationality

$\bullet\;$ Limited knowledge and/or computational ability

$\bullet\;$ Selfish motives

The Gambler's Ruin Paradox

$\bullet\;$ Related to St. Petersburg paradox [6]

$\bullet\;$ Gambler playing a ``double or nothing'' type game repeatedly against an infinitely rich adversary (multiplicative stochastic process).

$\bullet\;$ Chance of winning each time is p (known by gambler).

$\bullet\;$ In each iteration gambles a fraction r of wealth.

$\bullet\;$ Wealth after t iterations is W_t.

$\bullet\;$ Aside: can also be interpreted as a simple market model with one risky asset (price fluctuations as described above) and one riskless asset paying no interest. r describes portfolio.

$\bullet\;$ Expected wealth is

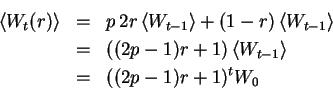
$\begin{eqnarray*}\left\langle{W_t(r)}\right\rangle & = & p\,2r\left\langle{W_{t-... ...eft\langle{W_{t-1}}\right\rangle \\ & = & ((2 p-1)r + 1)^t W_0 \end{eqnarray*}$

$\bullet\;$ Naive goal is to maximize $\left\langle{W_t}\right\rangle$ w.r.t. r:

\frac{1}{2}$} \\ 0 & \mbox{if $p < \frac{1}{2}$} \\ \mbox{irrelevant} & \mbox{if $p = \frac{1}{2}$} \end{array} \right. \end{displaymath} */ ?> $\begin{displaymath}r^* =\left\{\begin{array}{ll} 1 & \mbox{if $p > \frac{1}{2}$... ...rrelevant} & \mbox{if $p = \frac{1}{2}$} \end{array} \right. \end{displaymath}$

$\bullet\;$ If \frac{1}{2}$ */ ?> $p > \frac{1}{2}$ then ``rational'' gambler will wager everything.

$\bullet\;$ But must eventually lose (if p<1):

0) = \lim_{t\rightarrow\infty} p^t = 0 \end{displaymath} */ ?> $\begin{displaymath}\lim_{t\rightarrow\infty} P(W_t(1)>0) = \lim_{t\rightarrow\infty} p^t = 0 \end{displaymath}$

$\bullet\;$ Problem arises from heavy weighting of extremely unlikely events.

$\bullet\;$ Expectation maximization is a poor choice for modelling rational behaviour. So what is ``rational''?

Alternatives

Minimizing risk

$\bullet\;$ Maximizing expectation is too risky. Instead, might want to minimize risk of eventual ruin.

$\bullet\;$ If r<1 then will never gambler will never lose all wealth so let's define ruin as a net loss W_t < W₀. (Could also define ruin by granularity of money (eg. 1 penny) with the same conclusions.)

$\bullet\;$ Goal is to minimize P(W_t(r) < W₀) (for t large).

$\bullet\;$ For large t wealth distribution is roughly log-normal (because random walk on log-scale; will be discussed later).

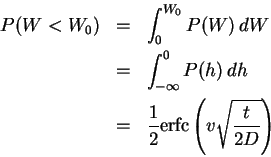
$\begin{eqnarray*}P(W < W_0) & = & \int_0^{W_0} P(W)\,dW \\ & = & \int_{-\infty... ... = & \frac{1}{2} \mbox{erfc}\left( v \sqrt{\frac{t}{2D}} \right) \end{eqnarray*}$

where $h = \ln (W/W_0)$ and P(h) is normally distributed with mean vt and variance Dt (also to be discussed later).

$\bullet\;$ Solution becomes clear from the probability distribution itself (with v and D expanded in terms of p and r).

$\includegraphics[width=\columnwidth]{ruin.ps}$

$\bullet\;$ Minimize risk by choosing

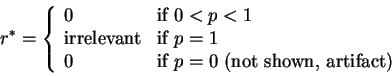
$\begin{displaymath}r^* = \left\{ \begin{array}{ll} 0 & \mbox{if } 0<p<1 \\ \m... ...ox{if } p=0 \mbox{ (not shown, artifact)} \end{array} \right. \end{displaymath}$

$\bullet\;$ So, in this interpretation, ``rational'' behaviour is to never gamble unless p=1. Too safe?

Utility function

$\bullet\;$ Agent values utility rather than wealth U(W).

$\bullet\;$ Utility is increasing, concave function ( 0$ */ ?> $U^\prime > 0$ , $U^{\prime\prime} < 0$ ). Literature suggests particulars of utility function largely irrelevant.

$\bullet\;$ A popular choice in finance is exponential utility U_e(W)=-e^{-a

W}, or equivalently

$\begin{displaymath}U_e(W) = W_{goal}\left(1-e^{-W/W_{goal}}\right) \end{displaymath}$

$\includegraphics[width=\columnwidth]{Utility.ps}$

$\bullet\;$ W_goal can be interpreted as maximum conceivable wealth or goal wealth (determines riskyness). (For finite system W_goal must be not be greater than all available wealth.)

$\includegraphics[width=\columnwidth]{chgrey.ps}$

$\bullet\;$ Consider a single iteration. Goal is to maximize expected utility

$\begin{displaymath}\left\langle{U(W_{t+1}(r))}\right\rangle = p\,U((1+r)W_t) + (1-p)\,U((1-r)W_t) \end{displaymath}$

$\bullet\;$ Solution: optimal investment fraction r^* is

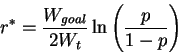
$\begin{displaymath}r^* = \frac{W_{goal}}{2 W_t} \ln \left( \frac{p}{1-p} \right) \end{displaymath}$

$\bullet\;$ r^* changes with each iteration as W_t changes. Decreases as wealth increases to W_goal.

$\includegraphics[width=\columnwidth]{r_opt-utility.ps}$

$\bullet\;$ Non-trivial solution for 1/2<p<1.

$\bullet\;$ Gamblers are still ``irrational'' because they will always gamble their entire wealth (r^* =1) when the chance of winning is greater than

$\begin{displaymath}p_{sucker} = \frac{1}{1+e^{-2 W_t / W_{goal}}} < 1 \end{displaymath}$

Kelly Utility

$\bullet\;$ Also common in the literature is the generalized Kelly utility [7]

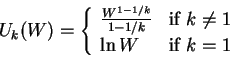
$\begin{displaymath}U_k(W) = \left\{\begin{array}{ll} \frac{W^{1-1/k}}{1-1/k} & ... ... } k \neq 1 \\ \ln W & \mbox{if } k = 1 \end{array} \right. \end{displaymath}$

$\bullet\;$ k=1 utility equivalent to $k\rightarrow 1$ because derivatives $\partial_W U$ the same. Absolute value doesn't matter for optimization.

$\bullet\;$ Kelly [8] originally hypothesized just the logarithmic form. Was generalized to $k\neq 1$ later.

$\bullet\;$ The advantage over previous utility is that there is no arbitrary cut-off wealth W_goal, but there is a parameter k (the Kelly parameter). Meaning will become clear.

$\bullet\;$ Again, goal is to maximize expected utility

$\begin{displaymath}\left\langle{U(W_{t+1}(r))}\right\rangle = p\,U((1+r)W_t) + (1-p)\,U((1-r)W_t) \end{displaymath}$

which gives

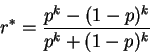
$\begin{displaymath}r^* = \frac{p^k - (1-p)^k}{p^k + (1-p)^k} \end{displaymath}$

$\includegraphics[width=\columnwidth]{r_opt-kelly.ps}$

$\bullet\;$ Kelly parameter k is ``riskyness''. k<1 = risk-adverse, k>1 = risk-prone. 1/k is ``risk aversion''.

$\bullet\;$ Kelly utility is more ``rational'' because r^* =1 iff p=1.

Median value

[9,10]

$\bullet\;$ Perhaps using the expectation value is an unfortunate choice. Often the median value is a more typical realization. Then a rational goal might be to try and optimize the median value of the future wealth.

$\bullet\;$ Median W_med is defined as point with equal probability of greater or lesser values:

W_{med}) = P(W P(W>W_med) = P(W<W_med) = 1/2

$\bullet\;$ To derive the median value we must recognize that the wealth W_t follows a multiplicative random walk

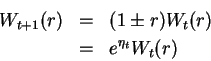
$\begin{eqnarray*}W_{t+1}(r) & = & (1\pm r) W_t(r) \\ & = & e^{\eta_t} W_t(r) \end{eqnarray*}$

where $\eta$ is distributed via

$\begin{displaymath}\pi(\eta) = p\,\delta(\eta-\ln(1+r)) + (1-p)\,\delta(\eta-\ln(1-r)) \end{displaymath}$

$\bullet\;$ Use log-scale to get additive noise

$\begin{displaymath}h_t = \ln W_t \end{displaymath}$

$\begin{displaymath}h_{t+1} = h_t + \eta_t \end{displaymath}$

$\bullet\;$ Random (biased) walk so, after many iterations, P(h,t) approaches a Gaussian distribution with drift velocity v and dispersion D

$\begin{displaymath}v = \left\langle{\eta}\right\rangle = p\ln(1+r)+(1-p)\ln(1-r) \end{displaymath}$

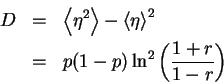
$\begin{eqnarray*}D & = & \left\langle{\eta^2}\right\rangle - \left\langle{\eta}\... ...\rangle^2 \\ & = & p (1-p) \ln^2\left( \frac{1+r}{1-r} \right) \end{eqnarray*}$

$\bullet\;$ Median (and average) of h linear in time h_med = v t.

$\bullet\;$ Median of wealth is

W_med = W₀ e^h_med

by definition, because

$\begin{displaymath}\frac{1}{2} = \int^\infty_{h_{med}} P(h) dh = \int^\infty_{W_{med}=W(h_{med})} P(W) dW \end{displaymath}$

$\bullet\;$ Goal is to maximize median (typical) wealth W_med w.r.t. r

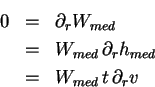
$\begin{eqnarray*}0 & = & \partial_r W_{med} \\ & = & W_{med}\,\partial_r h_{med} \\ & = & W_{med}\,t\,\partial_r v \end{eqnarray*}$

which has solution

r^* = 2 p - 1

$\bullet\;$ Same solution we saw for the Kelly utility function (k=1). Optimizing Kelly utility equivalent to optimizing median value.

Comparison

Mapping

$\bullet\;$ For exponential utility, must update r^* with each iteration. If we instead update W_goal via W_goal = f_goal W_t for some multiplier f_goal then r^* constant.

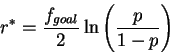
$\begin{displaymath}r^* = \frac{f_{goal}}{2} \ln \left( \frac{p}{1-p} \right) \end{displaymath}$

$\bullet\;$ Can map exponential utility U_e onto Kelly utility U_k by equating r^* yielding

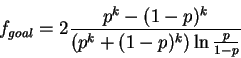
$\begin{displaymath}f_{goal} = 2 \frac{p^k - (1-p)^k}{\left( p^k + (1-p)^k \right) \ln\frac{p}{1-p}} \end{displaymath}$

$\includegraphics[width=\columnwidth]{mapping.ps}$

$\bullet\;$ Aside: regardless of riskyness k, for p>1/2, f_goal is bounded in order that agent remain ``rational'' (r^*<1)

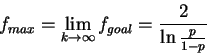
$\begin{displaymath}f_{max} = \lim_{k\rightarrow\infty} f_{goal} = \frac{2}{\ln\frac{p}{1-p}} \end{displaymath}$

Simulation

$\bullet\;$ All approaches explored (neglecting trivial solutions) so far reduce to two models: U_e (W_goal=constant) and U_k.

$\bullet\;$ Simulation shows iterated wealth of two exponential utilities (W_goal = 1/2 and 2) and three Kelly utilities (k = 1/2, 1 (log) and 2). Used p=0.6 and W₀=1 and all agents used same history of wins/losses.

$\includegraphics[width=\columnwidth]{sim-zoom.ps}$

$\bullet\;$ All but risky k=2 Kelly utility performed well over short term

$\includegraphics[width=\columnwidth]{sim.ps}$

$\bullet\;$ Fixed W_goal exponential utilities underperform (as expected) over long time. They can also crash (W_t=0) if wealth gets too low (not seen in this realization).

$\bullet\;$ k=1 (log) has best performance long-term but safe k=1/2 also good.

Conclusions

$\bullet\;$ Asked question ``How do we model rational agents?''

$\bullet\;$ Looked at gambler playing a ``double-or-nothing'' type game.

$\bullet\;$ Tricky because multiplicative process.

$\bullet\;$ Maximizing expectation too risky.

$\bullet\;$ Minimizing risk too safe.

$\bullet\;$ Common (exponential) utility can be too risky (and contains arbitrary scale).

$\bullet\;$ Generalized Kelly utility favourable.

$\bullet\;$ Maximizing median value equivalent to (original) Kelly utility.

$\bullet\;$ Median and expected values can be very different in multiplicative processes.

$\bullet\;$ Simulations suggest optimizing median value best. But smaller Kelly number can be just as good (and safer) on short time-scales.

$\bullet\;$ Maslov and Zhang [11] proved k=1 is on borderline of riskiness for similar model.

$\bullet\;$ Exercise: Prove Kelly utility (k=1) optimal as $t\rightarrow\infty$ [12].

Bibliography

1

D. Challet and Y.-C. Zhang (unpublished).

2

N. F. Johnson et al., cond-mat/9802177 (unpublished).

3

N. F. Johnson, P. M. Hui, R. Jonson, and T. S. Lo, cond-mat/9810142 (unpublished).

4

N. S. Glance and T. Hogg, (ftp://parcftp.xerox.com/pub/dynamics/computationalSocialDilemmaAIJ.ps) (unpublished).

5

N. S. Glance and B. A. Huberman, Sci. Am. 270, 76 (1994).

6

W. Feller, An Introduction to Probability Theory and its Applications (Wiley, New York, 1950), Vol. 1.

7

M. Levy, H. Levy, and S. Solomon, J. Phys. I France 5, 1087 (1995).

8

J. L. Kelly, Bell Syst. Tech. J. 35, 917 (1956), (http://www.bjmath.com/bjmath/kelly/kelly.pdf).

9

M. Marsili, S. Maslov, and Y.-C. Zhang, cond-mat/9801239 (unpublished).

10

S. Maslov and Y.-C. Zhang, cond-mat/9801240 (unpublished).

11

S. Maslov and Y.-C. Zhang, cond-mat/9808295 (unpublished).

12

P. A. Samuelson, Proc. Nat. Acad. Sci. USA 68, 2493 (1971).

About this document ...

Modelling Intentionality: The Gambler

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

The command line arguments were:
latex2html -dir /home/blok/public_html/p510gambler -split 0 p510gambler.

The translation was initiated by Hendrik Blok on 1998-12-08

Hendrik Blok
1998-12-08