Last week we examined analysis of two dependent or related samples. This week we turn to the case of independent samples. The approach for the two situations is quite different, although both types of tests rely on the t-distribution for parametric data. Just as last week, data that is ordinal can be analyzed using tests based on a binomial approach to ranked data. This ordinal approach can also be used for interval or ratio data when we cannot meet the assumptions of parametric testing.

This week we will also examine procedures that allow us to estimate the power of our tests. This approach lets us gauge the amount of difference we require between our samples and the size of samples we will need to provide a reasonable chance of rejecting the null hypothesis.

Previously, we showed that if we randomly take a large number of samples of size n from a normal population, then the distribution of sample means () will also be normally distributed. Similarly, if we take a sample from each of two populations, then the distribution of possible values for the difference between the sample means (i.e.1 - 2) will be normal. The parametric mean of this population of differences (m 1 - m2) will be equal to the difference between the parametric means of the two populations from which the samples were originally drawn. If the two populations are the same, there will be no difference in their parametric means (i.e., m1 - m 2 = 0).

Instead of calculating the deviation of a sample mean from a parametric mean, as in the one-sample case, the deviation of the difference between two sample means and the true difference between the means of the populations represented by the samples is determined in the two-sample case, (1 - 2)- (m1 - m 2). If the null hypothesis states that the true difference between the means of the populations is 0, then the deviation calculated is simply the difference between the sample means; however, it is possible to test a null hypothesis in which the magnitude of the true difference between two population means is some value other than zero (e.g. m1 - m 2 = 2.63).

To finish our calculation of the 2 independent sample t, we divide the mean difference by the standard error of the difference. The standard error of the difference between means is calculated by first taking a weighted average of the variances of the two samples, referred to as a pooled variance. We divide this pooled variance by each sample size and take the square root to turn it into a standard error.

In summary, the quantity

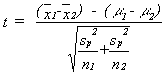
will follow a t-distribution similar to that of the one-sample case. Since two samples are involved and one parameter estimate (the sample mean) is required to calculate the standard deviation of each sample, this t-statistic has (n1 - 1)+(n2 - 1) = n1 + n2 - 2 degrees of freedom.

There are three main assumptions for a 2 independent sample t test. In addition to the requirement that both samples are taken at random from normally distributed populations, the two-sample t-test assumes that the two populations have equal variance. This assumption should be tested (as should normality). If the sample variances are unequal, then the pooled variance is a poor estimate of the population variance, making the t test invalid. This assumption of equal variance can be easily tested by hand by using an F test. The F test simply involves dividing the larger sample variance by the smaller sample variance. The resulting F value is compared to a table of critical F values to determine if the larger variance is significantly larger. The null hypothesis for this test is that the variances are equal, which would produce an F value of 1.00. There are a number of other, more complex tests of variance, including Bartlett's test, Levene's, O'Brien's and the Brown-Forsythe test.

Often, we find that the two populations have unequal variances. If this is the case, then we use the individual variances of the samples in the calculation of the t-statistic rather than the pooled variance. This version of the t test is known as Welch's approximate t:

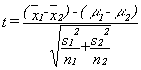
The critical value of t used in the test has a complex weighted calculation of degrees of freedom (because we didn't pool our variance estimates, we have to bias our answer towards the more conservative variance estimate):

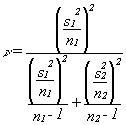
Confidence intervals for the difference between two independent means are calculated as the sample mean plus or minus the standard error of the mean difference times the critical t value for our alpha and degrees of freedom:

When we meet the assumptions of normal populations and equal variances, the standard error and degrees of freedom for this interval are calculated just as if we were doing a 2-sample t test. If the variances are unequal, as shown by an F test (or the variance tests carried out by JMPin), then we must use the unpooled standard error calculation and degrees of freedom calculation from a Welch's approximate t test. If the distributions are not normal, the confidence intervals are not valid and should not be used.

If our examination of the data suggests there is not normality at the population level and sample sizes are too small to invoke the central limit theorem, a number of non-parametric equivalents to the t test are available. The Mann-Whitney U test works on the ranks of the data, and under optimal conditions is about 95% as powerful as a 2 sample t-test. Other options include the van der Waerden test, which is the most powerful non-parametric option if the data is normal (which is almost never the case when you want to do a non-parametric test), and the median test, which is considerably weaker except for exponentially distributed data.

For the last few weeks you have heard us make statements such as the Mann-Whitney U test is about 95% as powerful as the 2 independent sample t test under optimal conditions. How did we come up with these numbers? Power analysis lets us estimate the ability of a test to reject the null hypothesis. In order to carry out a power analysis we must have some prior information about the populations we are studying. Generally, we need information on four characteristics: our desired alpha level, sample sizes, sample standard deviation, and the amount of difference between the samples. If you can supply JMP with all of this data (or at least your best guesses), it can provide you with an estimate of the power of a statistical test.

1. The a level (type 1 error rate). The a level and b level are inversely related. If an alevel greater than 0.05 is specified for a hypothesis test then the probability of a type 2 error (b ) will be lessened since it will take less of a difference between means to reject the null hypothesis. Conversely, if an a level less than 0.05 is specified, the b level will be higher.

2. The sample size (n). As sample size increases the probability of committing a type 2 error decreases. The probability of a type 1 error stays constant at our specified a level regardless of sample size.

3. The variability of our data. If all of our data points are very similar, it will be easier to detect a difference between our samples than if our data is highly variable. In this latter case, the difference between the samples will be obscured by the wide range of values possible from each of the populations.

4. The effect size or the true difference between the populations in our null and alternative hypothesis. This can be conceptualized most easily with the two sample t-test. When we are testing the difference between two population means the null hypothesis usually states the means are equal and the alternative hypothesis states that they are not. If the two means differ by a very small amount it will be harder to reject the null hypothesis even though the means might actually be different. The effect size is an unknown quantity and therefore power of a test can only be approximated. (If it were known there would be no reason to do a statistical test!). When a power analysis is done the experimenter takes a best guess at effect size. An example of this would be if we were doing a study of the effects of food on the weight of worms. If we feed one group of worms four times as much food as the other and tested the difference in weight between the two groups at the end of the experiment, we might expect the heavily fed group to be four times as large as the other. So a plausible guess of effect size might be four times the weight of the control group. Obviously, if we did the same experiment with humans we would probably not see such a large effect size! The experimenter should design a study to maximize effect size and therefore give the resulting tests more power.

Another factor that determines the power of a test is the type of test used. For example, nonparametric tests are often used when the assumption of normality cannot be met. These tests make no assumptions about the underlying distribution of the data. However, non-parametric tests are usually less powerful than parametric tests.

In theoretical terms, the power of a test is its ability to reject a false null hypothesis. Previously, we have explained that beta, the chance of a Type II error, is the chance of failing to reject a false null. It follows from this that beta is exactly equal to 1 - power. So estimating power also lets us estimate our chance of a Type II error.

Power analysis lets us estimate our ability to find a real difference between samples. It can tell us if our samples our too similar to have a reasonable chance of finding a difference for a specific sample size. Alternatively, if we have an estimate of the difference between the samples, we can predict how big our sample sizes should be to provide a reasonable chance of finding a difference.

2 Independent Sample t Test - To use the t-distribution to test a null hypothesis based on two samples, we must enter our data as two separate columns. One column must be all of the data from both samples, while the second column must be a listing of the sample to which each data point belongs. We can fit Y by X for these columns to carry out a two independent sample t test. Use the nominal column (the column showing from which sample the values come) as your X variable, and the continuous data variable as your Y. This will force you into the one-way ANOVA options and will produce a display showing the two samples side by side. Click on the Red Arrow just above this display. Clicking on this button will open up a sub-menu that will include the option for comparing means via an ANOVA or t test. Choose means, ANOVA/t test to display the 2 independent sample t test.

Confidence Interval for the Difference between Means - The upper and lower limits to the 95% confidence interval for the difference between the means are displayed in the t test box, once you have carried out a 2-sample t test. JMP does not calculate a Welch's confidence interval.

Analysing subsets of the data - To test if the two individual samples appear normal, you will have to work with subsets of the data. Choose Analyze -> Distribution as usual. Select the column on which you wish test normality. This time, however, also select the nominal column (that tells you which sample your data came from) and enter it as the By response. This should produce individual histograms for each sample, so that each can be tested for normality.

Variance Testing - To test the variances, choose unequal variances from the analysis sub-menu opened up after you have selected a t test as described above. The resulting display includes the Bartlett's, Levene's, O'Briens and Brown-Forsythe tests of variance, as well as the Welch's approximate t test. Newer versions of JMP also carry out a simple 2 sample F test. All five of the variance tests are extremely powerful, however, and any of them will indicate whether there is a problem of unequal sample variances.

Welch's Approximate t Test - From the same results box that you produced to test the sample variances, you can get the values for the Welch's t test. Since the program is designed to work with two or more samples, the display includes both the t test and the more general F test (the same test but for more than 2 samples). The probability associated with both tests should be identical.

Non-parametric Testing - JMP provides several options for non-parametric tests of the data. The Mann-Whitney U test is listed here as the Wilcoxon test (the Mann-Whitney U test, Wilcoxon rank sum test and the Kruskal-Wallis test which we will discuss next week have different calculations but turn out to be theoretically equivalent). Click on Non-Parametric -> Wilcoxon test to carry out this analysis. The van der Waerden's test, the Median test and the 2 sample Kolmogorov-Smirnov tests are alternate choices, but the Mann-Whitney/ Wilcoxon/Kruskal-Wallis test is the most powerful non-parametric option for most data sets.

Power Analysis - Once you have carried out an ANOVA or 2 sample t test, you can get information on the power of the analysis by clicking on the button beside the One-way ANOVA title. Clicking on this button will give you details on power. When you first open the power details dialog box, a set of values will be provided to you. These are defaults for the alpha value, the sigma or standard deviation (estimated from your samples), the delta value (the difference between samples measured in standard deviations - again this default value is taken from your data), and n, the sample size (from your data).

You can replace these default values with values that you would like to use for your calculations. You can see the effects of increasing or decreasing alpha, of changing the difference between means (delta) or any or all of the four characteristics listed.

You can do a basic power analysis by simply using the defaults provided by the computer. You can also track the changes between a pair of values by having the computer gradually change one or more characteristics. Pick the first value you would like to use in your analysis (the from value). You can use the defaults pre-calculated from your sample data by the computer or change the from value to any number you would like. Next pick a to value, the number you would like to see the computer use as the end of the calculation sequence. Finally, pick the increment or by value, the amount by which the computer will increase or decrease the from characteristic in each step, as it moves towards the to value.

Once you have set a range of characteristics for which you would like to see a power analysis, you can have the computer solve for the power of the statistical test given the characteristics you have inputted by checking the solve for power choice. Alternatively, you can solve for the smallest sample size needed to provide a specific power, by checking the solve for least significant number box. You can also solve for the minimum detectable difference between samples by checking the least significant value box. Finally, you can calculate an adjusted power estimate, which removes some of the bias we introduce to our analysis by basing all of our estimates on our sample. Carry out your chosen analysis or analyses by clicking on the done box.

Once you have done the analysis, the computer will show you a table of the results and display a Red Arrow below the table. Clicking on this button will display a graph of your results.

1. In order to determine conservation strategies for endangered species, biologists must decide whether animals in different regions represent distinct sub-species. In a study of Mexican ducks (Anas diazi), researchers compared wing lengths of birds from northern and southern regions as an indicator of speciation. The data are stored in a file named Anas in the shared directory.

2. In a study of resource use by bobcats and coyotes in Oregon, a researcher radio-collared a random sample of each predator and determined their annual average home range sizes (km²). The data are stored in a file named bobcoy.