UBC - BIOLOGY 300

This week you will learn about hypothesis testing for the first time. Forming and testing hypotheses is one of the most basic approaches to statistical analysis and the scientific method in general. For the purpose of statistical testing of a hypothesis it is normal to formulate a pair of hypotheses: the null hypothesis (Ho) and the alternate hypothesis (Ha). These two hypotheses are mutually exclusive; that is, if one is true, then the other must be false. At the same time they are mutually inclusive, meaning that between the two hypotheses, all possible outcomes are covered.

One of the most fundamental concepts of the scientific method is that proof of a theory is impossible since we do not fully understand the universe. As a result, we never try to prove theories or hypotheses. We can, however, disprove hypotheses, and most statistical tests are designed to disprove the null hypothesis. We set up the null hypothesis specifically so that we can disprove it. The alternate hypothesis, it’s opposite counterpart, is usually the idea that we would like to prove (but can’t because proof is impossible).

Even disproving the null hypothesis, sometimes known as the hypothesis of no interest, is difficult. Since we are usually working with samples from a larger population, there is uncertainty about our calculated statistics. As a result there is always a chance of error. There are two types of errors that we commonly make: Type I errors occur when we reject the null hypothesis incorrectly. Type II errors occur when we fail to reject the null hypothesis even though we should. The chance of making a Type I error is known as alpha, while the chance of a Type II error is beta. We typically set our alpha level when we decide what level of risk we are willing to risk of being wrong. The beta level is unknown, since it occurs when we miss a difference in our analyses that was totally unexpected.

Type I errors occur because most distributions have tails that continue on to infinity. This means that any level of deviation from the mean is possible, although extreme deviations from the mean are highly unlikely. When we specify an alpha level, we are choosing a point at which we declare that any value more extreme is too unlikely a result if we are sampling from our specified distribution. This is the level of risk we are willing to live with because only rarely will we sample from the extreme end of a tail of our distribution. When we sample from this area and see an extreme deviation, we reject our null hypothesis and declare that the data do not seem to come from our expected distribution; however, we just happened to be unlucky in our sampling, and made a Type I error.

The fact that most distributions have two tails leads to differences in the way we formulate our hypotheses. When we know little about our sampled data and the underlying distribution, we will reject the null hypothesis whenever we obtain sample statistics that are extremely different from what we expect (when there is a low probability that our sample comes from our expected distribution). When we will reject for any extreme difference, we are generating two-tailed hypotheses, since we will reject the null hypothesis for any statistics that are far out into either tail of the distribution.

Sometimes we have some knowledge of the way our experiments should work and in this case we can make more specific predictions. If, for instance, we expect results that are higher than a theoretical mean, we can formulate a set of one-tailed hypotheses, meaning that we will reject the null hypothesis and lend support to our alternate hypothesis only if there is an extreme deviation from the theoretical value in the positive direction. That is, we will reject the null hypothesis only if we see values in the extreme ends of the positive tail of the distribution.

Another important concept in hypothesis testing is the number of degrees of freedom available for our test. You may have encountered this idea already in the formula for sample standard deviation. In that instance our statistic is calculated with n - 1 degrees of freedom because we use another statistic (the sample mean) to derive the sample standard deviation. The degrees of freedom for a hypothesis test are used to determine the shape of the theoretical distribution, since many distributions (like normal, binomial, Poisson and others) can take on different shapes as their parameters change. Using JMP most of these calculations are built into the computer, but very occasionally you will have to override the automatic calculations due to the nature of your experimental design.

A goodness of fit test is a way to test whether sample values have been drawn from a population with a known statistical distribution (such as the uniform, normal, binomial, Poisson, etc.). The most commonly used goodness of fit tests are the Chi-squared (sometimes known as Pearson’s Chi-squared), the G-test (also referred to as the log-likelihood ratio) and Kolmogorov-Smirnov tests. The underlying principle of all of these tests is similar: the frequency of occurrence of observed values is compared with the expected frequency derived from the equation for our expected distribution. If the difference is too great to be attributed to chance, we conclude that the sample did not come from the expected distribution. The type of data determines the particular test used. Chi-squared and the G tests are used with discrete, nominal scale data, while the Kolmogorov-Smirnov test can be used with data in any measurement scale (ratio, interval, ordinal or nominal scale) and that is either discrete or continuous. Generally, though, Chi-squared and G are preferred for discrete data, while the Kolmogorov-Smirnov test is most appropriate for continuous data.

JMP also calculates two similar tests for continuous data: the Kolmogorov-Smirnov-Lilliefors test and the Shapiro-Wilks test. Both tests are more powerful (able to detect differences between observed and expected) than the plain Kolmogorov-Smirnov test, with Shapiro-Wilks being the most powerful for many situations. We will deal with goodness of fit for continuous data in a future lab and concentrate on categorical or nominal data this week.

The most basic of the goodness of fit tests is the Chi-squared test (chi rhymes with sky for those of you unfamiliar with Greek pronunciation). This test lets us generate an index of deviation between our observed samples and our hypothetical, expected distribution. Since we could have positive or negative deviations which would cancel each other out if we just added up the deviations, we square the deviations between each observed and expected frequency, then scale the deviations by the expected frequencies before we add them up to generate our index of deviation. The formula for Pearson's chi-squared is:

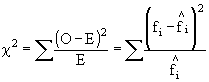
Similarly the formula for G ( the likelihood ratio) is:

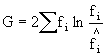
Both the G test and Pearson’s Chi-squared are equations that approximate the theoretical Chi-squared distribution. They are slightly different approximations, each of which has its advantages and disadvantages in specific context. For the purposes of our lab you can treat them as interchangeable. If the two tests give you different results (one suggests that observed and expected are different, while the other fails to find a difference), the conservative approach suggests you should rely on the test that fails to find a difference.

The degrees of freedom for goodness of fit tests are affected by the use of information from our sample. This forces our choices for expected values and reduces the available degrees of freedom for our test. For Chi-squared and G tests, the degrees of freedom is k (the number of categories) minus one degree of freedom for each statistic used to derive our expected values. Typically, our degrees of freedom equals k - 1, because we force our expected values to add up to the same total as our observed values. Keeping observed and expected on the same scale allows us to most accurately gauge the amount of difference between the two sets of values.

Problems with Chi-squared and G tests

An important limitation to goodness of fit tests is that they can only show us whether our observed and expected values are significantly different. They are unable to tell us if the expected values for any category are significantly larger or significantly smaller. That is, they carry out a 2-tailed hypothesis test, looking for any difference between observed and expected, either a positive or a negative difference.

Another set of limitations is due to the approximations we use. When there is only a single degree of freedom for a chi-squared or G analysis the approximation is poor. In this case a correction (called a continuity correction) can be applied. You can learn more about this correction in your textbook. The approximations are also poor whenever expected values are small. Unfortunately, this problem can not be fixed by an adjustment to the equations. The only solution is to ensure that expected values are fairly large.

Work by a number of statisticians has produced a general rule of thumb for times when we can expect the approximations to true Chi-squared to be bad enough that we should not continue with our analysis. Whenever any expected value is less than 1, or when more than 20% of our expected values are less than 5, the approximation is very inaccurate. When this happens our only recourse is to group some of our categories together to increase the size of our expected values. JMP will occasionally warn you of small expected values, but the program is erratic in its monitoring of this problem, so you should always watch for this one yourself. JMP does not apply continuity corrections when there is one degree of freedom. Again, watch for this problem yourself.

The approximations to the chi-squared distribution are often used to test hypotheses where the data available for analysis consist of more than one variable. In this case, we can use a similar approach to goodness of fit testing to detect dependence or relationships between the two variables. This use of Chi-squared (and G) is known as a contingency test. We are looking to see if the values from one variable are dependent or contingent on the values from another variable. Our null hypothesis for a contingency test is always that the variables are independent from one another, or that they have no effect on each other.

In order to carry out a contingency test, we compare our observed results to those we would expect if the values are independent of each other. We arrange our data into a table with the variables on separate axes and derive Chi-squared values for each cell of our table. Basic rules of probability cause the expected value for each cell to equal the sum of all observed values in the row, times the sum of all observed values in the column, divided by the sum of all observed values (the rationale for this is provided in your textbook):

The degrees of freedom for a contingency test are always (R - 1)(C - 1). As soon as we know all but one expected value for a row we can determine the final expected row value since we force observed values to equal expected values. As soon as we know all but one expected value for a column we can similarly derive the final column value. This means that the final values in a row, and the final column of values are forced, non-independent choices and do not provide additional information or power for our hypothesis test. While they are still important for the calculation of our statistics they do not improve our power or ability to detect a difference between observed and expected values.

Contingency tests allow us to test the relationship between 2 variables no matter how many categories there are for each variable. Unfortunately, as with the one-variable goodness of fit tests, they can only test two-tailed hypotheses. They can not differentiate between positive and negative differences between observed and expected values.

When there are only two categories in each of the two variables (a two by two table of observations), JMPin carries out another test of the relationship which is more accurate and powerful. This test is called the Fisher’s exact test and can support both one and two-tailed hypotheses. The calculations for this test are extremely tedious and generally this test is only done when you have access to a good computer program. For the purposes of this week’s exercise we will examine two-tailed hypotheses only. See Zar for more information on one-tailed Fisher’s exact tests.

Chi-squared and G tests require you to have categorical or nominal data. They will only become accessible if you format your column’s modeling type to nominal. If you are entering names for your categories you will also have to convert the data type to character.

The data for most of these tests are most easily entered as frequency data. This means that it should be entered as two columns: the first is the category and could be a name or a number (litter size, phenotype or whatever is appropriate). The second column is the frequency of values in each of the categories from the first column. When we analyze this data using Analyze -> Distribution, add the first column as the one to be measured, and then choose the second column as the frequencies for the first column.

When you produce a histogram (actually a bar graph since this is discrete data), clicking on the Red Arrow beside the column name lets you test probabilities. A new sub-window will open up with a column showing the levels (the observed values), a column of estimated probabilities (how common these values were) and a column of empty boxes. Click on each of the empty boxes and fill in the expected value that corresponds to each observed value. If, for instance, we were testing whether our observations came from a uniform distribution, and we had 10 observations in 5 classes, we would expect that a uniform distribution would have 2 values in each class. Goodness of fit tests let us decide whether our observations fit these expectations.

Note that the computer offers you the option of using estimated probabilities for blanks or rescaling the values to add up to 100. Generally, you can ignore this, as you should not have any blank values.

The computer will provide us with the probability of observing the measured level of difference between observed and expected. It gives us the probabilities for both a Chi-squared test (Pearson's) and a G test (likelihood ratio). If the probability shown is greater than our alpha level (a) we fail to reject our null hypothesis that there is no difference between observed and expected. If the probability is lower than a we conclude that there is only a remote chance that this result could have happened by chance and therefore we reject our null hypothesis: we suggest that observed and expected differ because we are not sampling from the expected distribution.

While data for a goodness of fit test can be entered as two columns (one for the categories and one for the frequencies), they still consist of only one variable. Contingency testing is done on two (or more) variables. This data is also most conveniently entered as frequency data, so that tests of two variables will require 3 columns: one for the frequencies, and two for the corresponding categories in each variable.

In order to conduct a contingency test, choose analyze, then fit y by x. Designate your categorical variables as X and Y and the frequency variable as (surprise) the frequency variable. The computer will display a version of the contingency table along with the appropriate statistical values.

1. A common tool in studying life-history attributes of small mammals is to provide them with nest boxes in the field. These boxes can then be sampled periodically to measure the life-history attributes of individuals that use them. A researcher used nest boxes to measure litter size in the field mouse (Peromyscus maniculatus) in northern B.C. She randomly sampled 48 nest boxes with young and counted the number of live young (litter size) in each nest box. The following data were obtained:

2. In a breeding experiment, disease resistant, early maturing apple trees were randomly crossed with each other and produced 190 saplings of the types shown below:

3. A researcher was interested in phenotypic variation of the black-spotted stickleback (Gasterosteus wheatlandi) along the east coast of North America. Samples of these fish were collected north and south of Cape Cod. The number of lateral plates (hard, bony shields which are usually larger than scales) were counted and individuals classified as low- or high-plated phenotypes:

4. An experiment was undertaken to examine the effects of different fertilizer treatments on the incidence of blackleg (Bacterium phytotherum) in potato seedlings. A number of seedlings were examined for each treatment and classified as contaminated by blackleg or free: