The Lotka-Volterra Competition Model

In populations that have overlapping generations, the logistic curve is described by the logistic equation (Krebs p.161):

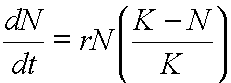
The Lotka-Volterra equations, which describe the competition between organisms, are based on the logistic curve. Each of these next two equations shows the effect of intra-specific (within a species) competition only (all numbers in the equation are the same).

For species 1:

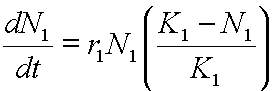
(Krebs p.180)

For species 2:

Now suppose that 10 individuals of species 2 have the same inhibitory effect on an individual of species 1 as does a single individual of species 1 (this would be an inter-specific, or between-species, effect). Then the TOTAL competitive effects on species 1 (intra- and inter-specific) will be equivalent to:

(N₁ + N₂/10) species 1 individuals

1/10 (in the case of this example) is the COMPETITION COEFFICIENT and is called a.

This is the per capita inter-specific competitive effect “ON species 1 OF species 2”.

The equivalent per capita effect for the 2^nd species, “ON species 2 OF species 1”, is b.

So the total inhibitory effect of individuals of species 1 (intra-specific force) and species 2 (inter-specific force) on the growth of population 1 will be:

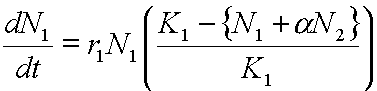
in which aN₂ ”converts” N₂ to a number of “N₁ equivalents”. Removing the inner brackets:

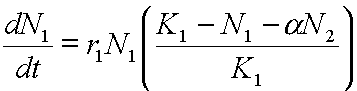
(Krebs p.181)

Thus there are two “sources of slowing” for the growth of species 1: its own density, and the density of the second species weighted by the second species’ relative impact.

For species 2, we have the equivalent formulation:

(Krebs p.181)

These two constitute the Lotka-Volterra model - a logistic model for two species.

The final step would to determine the conditions under which each population would be at equilibrium, that is the conditions under which dN/dt would be zero. In some cases only one population will be able to achieve an equilibrium stable density, and in other cases both can.

The various cases are summarized graphically on pages 182-183 in Krebs. Note that in some printings of the textbook, the intercept-point labels on the axes of these figures (12.1-12.3) are incomplete:

· where an intercept is labeled “K₁/”, it should read “K₁/a”;

· similarly, where an intercept is labeled “K₂/”, it should read “K₂/b”.

In the lecture, we will develop drawn models from scratch, since this is the most effective way to learn how to use the model.