Functional Responses, Holling’s Disk Equation, and Predation Modeling Outline

Predators may respond to changes in prey-abundance in several ways:

· by changing individual behaviour in the short-term (functional response)

· by learning, up to the scale of a predator-lifetime (developmental response)

· by grouping at sites of high prey abundance (aggregative response)

· by reproducing to take advantage of a growing prey population (numerical response)

Holling’s Disk Equation model focuses on the first option: how does a predator respond to changes in prey density (assessed by the number of prey which can be captured per foraging period at different densities)?

Assumptions: (many are unrealistic, but we’ll deal with this later)

w the model looks at a single individual predator in isolation

w only one prey type (species) is being attacked

w all prey individuals are identical/interchangeable (no age/sex/health/etc. variation)

w the predator thus takes the same period of “handling-time” to deal with each prey

w the number of prey caught is very small compared to the number available (i.e. no depletion)

w the predator is as hungry at the end as it was at the start (hunts just as hard)

w the total time available for foraging (per day, for instance) is constant

The model

Call the density (individuals per unit area) of prey available N . This is the main input-variable.

Call the total time spent foraging in a day T. (a constant for a given forager, varies by species)

Call the total time spent searching for prey T_s ; this will be made up of one or more variable-length bouts of searching, some ending with prey-capture and some not.

Call time spent handling a single prey item T_h . For a given pair of species, this is a constant.

A forager may catch no prey, or some prey, during a foraging period T; call the number of prey caught (eaten) N_e . This will be the main result-variable in the model. Thus the total time spent handling (eating) prey will be N_e(T_h) .

During the foraging period, the foraging predator will be spending all of its time either searching for prey, or handling captured prey. Thus the total foraging time is divided as follows:

( or, as we need below: )

Now consider, just using common sense, what might determine the number of prey caught (N_e):

n the more time spent searching (larger T_s), the more prey could be caught

n the more prey available in the area (prey density, N), the more prey could be caught

n the more “behaviourally efficient” the predator, the more prey could be caught

This last factor, efficiency, can be modeled as a coefficient or multiplier: call it C .

So we could roughly model the number of prey caught as:

We already derived above an expression describing T_s in terms of our other variables, so:

becomes

by direct substitution. If we multiply through to remove the brackets:

and then rearrange to get both of the terms containing N_e on the same side:

we can remove a common factor of N_e on the left side of the equation:

and then “cross-multiply”, moving the bracketed item over to the right side, thereby isolating the “result-variable” or dependent variable, N_e, on the left:

and finally rearrange to get the N term at the far right, since prey density is the model’s focus after all, and we usually want to show the main independent variable as the last one in the set of variables:

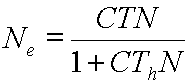
This is the basic form of the final disk-equation model, in a “y = a x”-type format.

Using the model

Krebs shows a graph on page 222 (Figure 13.16), and we will be drawing more graphs during lecture for further development of the ideas. This is part of the model’s use.

Different mathematically-calculated forms of the model (using the square of density, for example) can be used to generate different curve-shapes. We will not be going in this direction in Biology 303.

Another use of the model is (as with all models) to “explore the extremes” – what happens when the model is applied to extreme cases? Does it produce a biologically meaningful outcome? It is very much worth our time to do this. Here is a start.

Consider the following cases:

What happens when N is very small?

Since N measures density rather than absolute numbers, it can be a very small value, easily much less than 1 (e.g. 0.005 individuals/km²). If this is the case, then the CT_hN term in the denominator becomes small compared to the “1” (so the denominator approaches a value of simply 1, and can be ignored), and the whole equation approaches:

This should make a lot of sense: if few prey are present, almost all of T will be spent searching, but of course most of that will be unsuccessful searching! At the extreme, a forager might catch zero prey per time T, no matter its efficiency. Small N thus gives very small N_e .

What happens when N is very large?

As the N gets large, the “1” in the denominator becomes fairly insignificant compared to the CT_hN term, and so the model approximates:

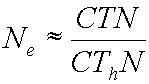, which simplifies by canceling to:

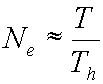
What does this mean? When the available prey are abundant, hardly any time need be spent in searching for each one; essentially the forager is surrounded by prey, which need only be picked up and handled. Thus nearly the entire T period is composed of handling-periods, and there will be a maximum number of prey which can be consumed, since T and T_h are both considered constants – basically an asymptote. This can be interpreted as evidence of saturation (but not physiological satiation, remember the model’s assumptions don’t allow that!).

You might want to think of other ways of stretching the model to extremes, as practice.

Limitations of the model

Basically all of the assumptions! The functional response model would work only if all the assumptions outlined above were met, and we know from basic commonsense principles that in many cases some or all of them cannot be met. To improve our understanding, then, we will be relaxing several assumptions (copied from the list at the start of this document), as follows:

Relaxing assumptions concerning prey-type characteristics:

w only one prey type (species) is being attacked

w all prey individuals are identical/interchangeable (no age/sex/health/etc. variation)

w the predator thus takes the same period of “handling-time” to deal with each prey

We will look at a model of optimal diet-selection or prey-type choice to relax this set. See pages 225-227 in Krebs.

Relaxing assumptions concerning prey depletion and predator satiation:

w the number of prey caught is very small compared to the number available (i.e. no depletion)

w the predator is as hungry at the end as it was at the start (hunts just as hard)

We will develop a graphical model of patch-use (Marginal Value theory) to relax these. This model approach is not covered explicitly in Krebs, but adds to our understanding usefully.

Relaxing assumptions concerning number of predators:

w the model looks at a single individual predator in isolation

We will develop (mostly graphical) Lotka-Volterra-type dynamic models of entire predator and prey populations in interaction with each other. Similar coverage is in Krebs, pages 207-212.