Two-Locus Selection Models
Clearly, one-locus models of selection are highly simplified depictions of how populations evolve over time.
Exact analyses with multiple loci are, however, extremely difficult if not impossible to obtain.
Even with just two loci, the dynamics are complicated and not completely understood. Results are generally limited in scope, focusing on particular fitness schemes.
Nevertheless, results from two-locus models are very important in determining what properties of the one-locus model are unique and so might not apply to the real-world situation in which a number of loci collectively interact to guide the formation of the individual.
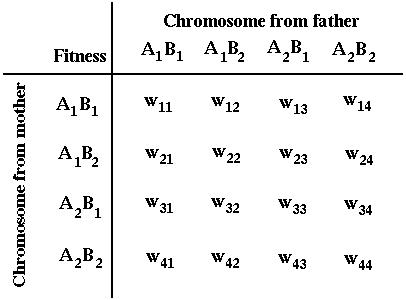
We will consider a model with two loci, A and B, with two alleles each: A1, A2 and B1, B2 respectively.
There are four possible combinations of these alleles on a chromosome:
Chromosome type: A1 B1 A1 B2 A2 B1 A2 B2
Frequency: x1 x2 x3 x4
[Note: x1 + x2 + x3 + x4 = 1]
We specify the rate of recombination between two loci by r.
[Note: Recombination may occur in any individual but it only changes the type of gametes produced if the parent was a double heterozygote.]
where the survival of a diploid individual depends on its genotype:
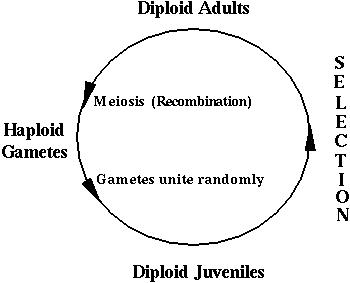
These gametes unite at random, creating all possible combinations according to their frequencies. Selection then acts on these diploid genotypes producing a new generation of adults. These adults undergo meiosis to produce the next generation of gametes.
These processes are illustrated in the following mating table:
For instance,
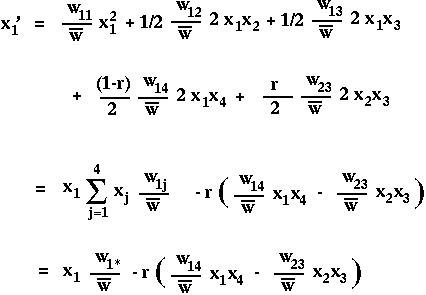
where we define
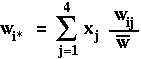
as the marginal fitness of allele i (the fitness that the allele experiences averaged over all genetics backgrounds) and where
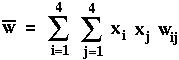
is the mean fitness of all members of the current population.
The equations describing selection in the two-locus diploid model are then:
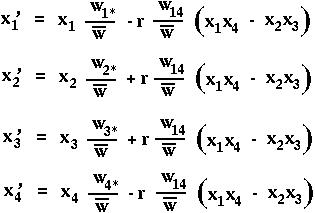
Notice that recombination only enters into these equations when multiplied by (x1 x4- x2x3). This term is known as the linkage disequilibrium, D.
Technically, D measures the difference in frequency between "coupling" (A1B1 and A2B2) and "repulsion" (A1B2 and A2B1) gametes.
More intuitively, D measures the difference between the observed and expected gamete frequencies:
x2 = pA1 pB2 - D
x3 = pA2 pB1 - D
x4 = pA2 pB2 + D
where pA1 is the frequency of allele A1 in the population (pA1 = x1+x2).
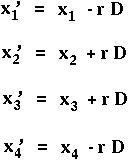
Let's first find out what happens to the disequilbrium over time.
What is D' = x'1x'4 - x'2x'3 ?
Linkage disequilibrium decays at a rate r every generation.
After an amount of time t, the expected amount of disequilibrium is D[t]=(1-r)t D[0].
Therefore, after enough time has passed, we expect to see little linkage disequilibrium between two neutral (=not selected) loci unless they are very tightly linked.
What is p'A1 = x'1+x'2 ?
In the absence of selection, allele frequencies remain constant.
For comparison, remember that in the one-locus model, a new allele would invade if it had a higher fitness.
Let's say that the population is initially fixed on A1B1 (x1=1) and that the system is perturbed such that some A1B2 (x2=epsilon2), A2B1 (x3=epsilon3), and A2B2 (x4=epsilon4) chromosomes exist within the population.
If we were to do a Taylor series of the equation for x'2 and keep only linear terms in epsilon, we would get:
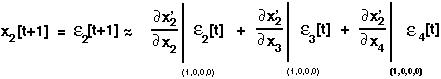
Repeating this for x'3 and x'4, leads to three linear equations in three variables (the perturbations), which we can write in matrix form:
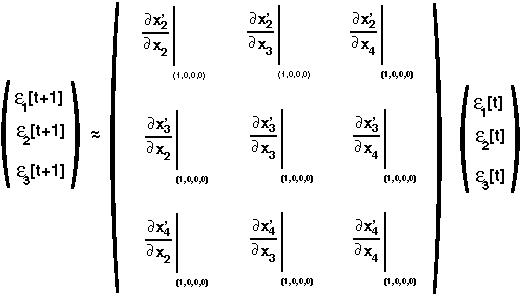
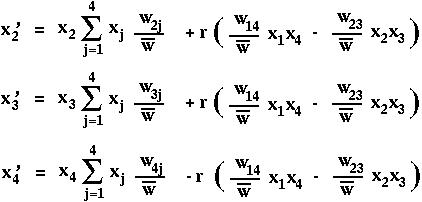
we can determine what all the partial derivatives are to get:
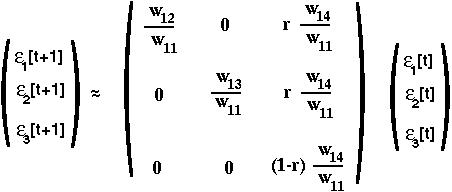
This is the local stability matrix for the two-locus selection model near the equilibrium with one chromosome fixed.
Since the eigenvalues of a triangular matrix are simply the diagonal elements:
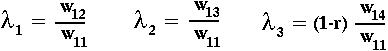
we learn that the fixation state with A1B1 present is unstable if ANY of the following hold:
This last condition tells us that beneficial gene combinations will invade only if there is tight enough linkage between the two loci (unless the new alleles are also beneficial on their own).
Back to biology 301 home page.