
Non-Linear Equations



We now turn our attention to models that describe the dynamics of a system in terms of NON-LINEAR equations in more than one variable.
With occasional exceptions, non-linear systems of equations do not yield general solutions (i.e. they are often intractable).
Other methods of analysing equations therefore become especially important, including


Model Parameters
Let
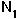 = # of individuals of species 1
= # of individuals of species 1
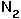 = # of individuals of species 2
= # of individuals of species 2
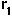 = intrinsic growth rate of species 1
= intrinsic growth rate of species 1
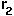 = intrinsic growth rate of species 2
= intrinsic growth rate of species 2
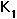 = carrying capacity of species 1 when species 2 is absent
= carrying capacity of species 1 when species 2 is absent
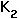 = carrying capacity of species 2 when species 1 is absent
= carrying capacity of species 2 when species 1 is absent


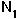 +
+ 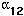
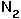
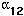 is called the COMPETITION COEFFICIENT measuring the
effect of an individual of species 2 on an individual
of species 1.
Similarly,
is called the COMPETITION COEFFICIENT measuring the
effect of an individual of species 2 on an individual
of species 1.
Similarly,
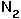 +
+ 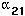
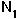
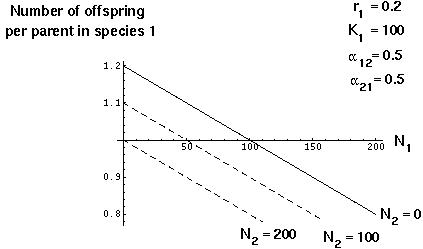
The assumption of the logistic model is that the number of offspring per parent decreases linearly with the number of individuals (of species 1) currently in the population.
With a second competing species also present, the number of offspring per parent depends not only on 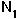 , but also on the value of
, but also on the value of 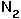 :
:
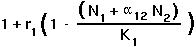


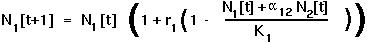
Similarly,
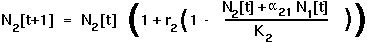
Continuous Model
In this case, it is assumed that the individual's contribution to the population growth rate is
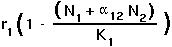 for species 1
for species 1
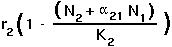 for species 2
for species 2
 for species 1
for species 1
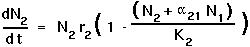 for species 2
for species 2
We'll focus on the discrete case in class.


In both the discrete and continuous cases,
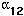 equals zero, then the dynamics of species 1 will follow the logistic equation we analysed before.
equals zero, then the dynamics of species 1 will follow the logistic equation we analysed before.
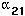 equals zero, then the dynamics of species 2 will follow the logistic equation we analysed before.
equals zero, then the dynamics of species 2 will follow the logistic equation we analysed before.
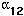 equals one, then individuals of species 2 compete for the resources of species 1 just as strongly as do members of species 1 (interspecific competition is as strong as intraspecific competition).
equals one, then individuals of species 2 compete for the resources of species 1 just as strongly as do members of species 1 (interspecific competition is as strong as intraspecific competition).
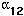 is negative, then the presence of species 2 increases the resources available to species 1.
is negative, then the presence of species 2 increases the resources available to species 1.
If both 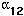 and
and 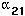 are negative, the species are said
to have a mutualistic relationship.
are negative, the species are said
to have a mutualistic relationship.
If 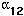 or
or 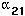 is negative and the other is zero (or very
nearly zero), the species are said to have a commensal relationship.
is negative and the other is zero (or very
nearly zero), the species are said to have a commensal relationship.
If one of the two is positive and one is negative, the species are said to have a parasitic relationship.
If both are positive, the species are said to have a competitive relationship.
 We will analyse the effects of competition (with
We will analyse the effects of competition (with 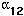 > 0 and
> 0 and
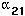 > 0) on the dynamics of two species.
> 0) on the dynamics of two species.


Preliminary Graphical Analysis
The first step of an analysis might be to graph examples to see what happens to each of the species under different parameter conditions:
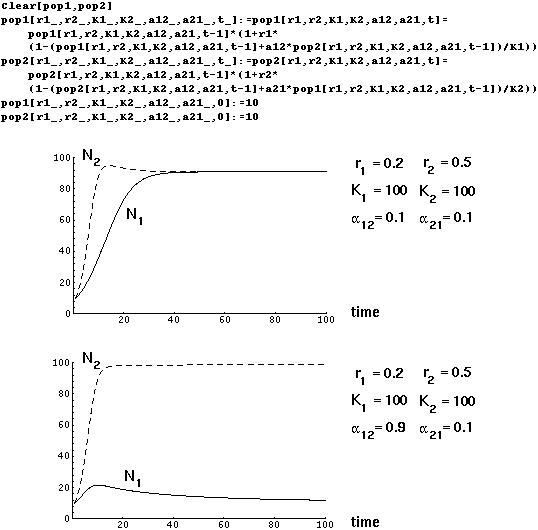
When 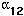 and
and 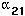 are small, both species approach an equilibrium level near their carrying capactities. If
are small, both species approach an equilibrium level near their carrying capactities. If 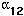 is much higher than
is much higher than 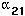 (species 2 impacts more strongly on the resources of species 1 than vice versa), then species 1 will be kept at low numbers by the competitive superiority of species 2.
(species 2 impacts more strongly on the resources of species 1 than vice versa), then species 1 will be kept at low numbers by the competitive superiority of species 2.


Such a graphical method is only useful for specific examples, however, and doesn't give us a general picture of what will happen and when.
Identification of Equilibria
As before, we determine equilibria by finding out when the variables will stay constant over time.
Unlike the case of a single variable and a single function, however, we must find an equilibrium solution where ALL of the variables remain constant over time.
For the continuous model of competition, this requires that d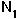 /dt = 0 AND that d
/dt = 0 AND that d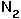 /dt = 0.
/dt = 0.
For the discrete model of competition, this requires that 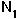 [t+1] =
[t+1] = 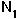 [t] AND that
[t] AND that 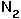 [t+1] =
[t+1] = 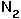 [t].
[t].
Setting 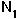 [t+1] =
[t+1] = 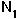 [t] =
[t] = 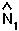 in the discrete equation for species 1 gives:
in the discrete equation for species 1 gives:
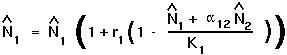
There are two ways in which this equation can be satisfied:



Setting 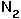 [t+1] =
[t+1] = 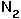 [t] =
[t] = 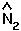 in the discrete equation for species 2 gives:
in the discrete equation for species 2 gives:
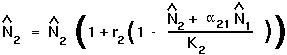
Again, there are two ways in which this equation can be satisfied:
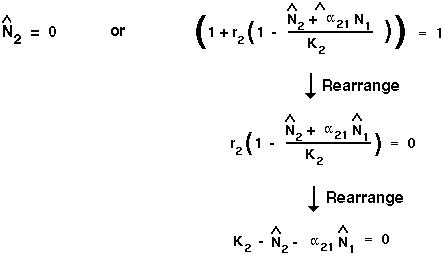
At equilibrium, there are four ways to ensure that both 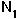 and
and 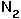 remain constant over time:
remain constant over time:
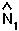 = 0 and
= 0 and 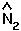 =0)
=0)
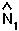 = 0 and
= 0 and 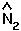 =
=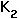 )
)
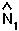 =
= 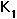 and
and 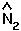 =0)
=0)


To get both species to persist at equilibrium requires that both

To solve both equations simultaneously:
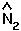 in terms of
in terms of 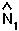 .
.
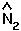 into the other equation.
into the other equation.
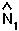 in terms of the parameters of the model.
in terms of the parameters of the model.
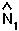 into one of the above equations to get an equation for
into one of the above equations to get an equation for 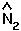 .
.

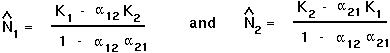
Only at this point will both species be present in constant numbers over time.