Eulimnadia

Evolution with three sexes

Eulimnadia texana is a clam shrimp, distributed throughout the southern United States. It is found in ephemeral freshwater ponds. During the dry season, the species survives by producing dessication-resistant eggs. After periods of rain, these eggs hatch and develop rapidly (generation time: 5-10 days).

Eulimnadia texana is an extremely unusual species in having three sexes (at least genetically). Sex in Eulimnadia is determined by a gene or gene region as follows:

SS Ss ss

Female Female Male

Females reproduce by one of two means: self-fertilization and/or sex with males. Males cannot self and females cannot fertilize one another.

Consequently, the following matings can occur:

Interestingly, the sex ratio varies from pool to pool, with males ranging from 0-35%.

A number of evolutionary questions arise in this system:

Why are males maintained?
What sex ratio is expected within the population?
What are the costs of inbreeding? outbreeding?

ABCs of Modelling

Step 1: Formulate the question

What information do you really want to know?
Boil the question down!

Step 2: Qualitatively describe the model

Start with the simplest, biological reasonable description
Make sure that results from the model can address the question

Step 3: Quantitatively describe the model

Define the variables in the model
Consider how the variables relate to one another
Define the parameters in the model
Consider whether any of the parameters are redundant

Step 4: Derive equations describing the biological system

Write down the equations (a diagram or table may help)
Perform checks (eg. do the relationships among the variables still hold?)

Step 5: Analyse equations

Make sure analysis addresses the question
Determine how general the results are

Step 6: Re-examine Assumptions

Consider alternatives to the simplest model
Expand model, if appropriate, and repeat steps 3-5

Step 7: Relate back to biology

Do the results answer the biological question?
Are the results counter-intuitive? Why?
Relate the results to data or to potential experiments

Modeling this Sex Determination System

Variable: "A quantity that may assume any one of a set of values"

u: frequency of ss males
v: frequency of Ss females
w: frequency of SS females

Parameter: "An arbitrary constant whose value describes a characteristic of a system"

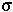1-: fitness of males relative to fitness of females
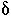1-: fitness of individuals produced by selfing
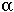: proportion of eggs that will be mated with male sperm when a male is encountered
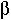: proportion of eggs not fertilized by males that are selfed

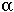For example, an SS female will encounter an ss male at a rate proportional to his frequency (u). The probability that one of her eggs will be fertilized by a male is then u*

(the probability of encountering a male times the probability of using his sperm).

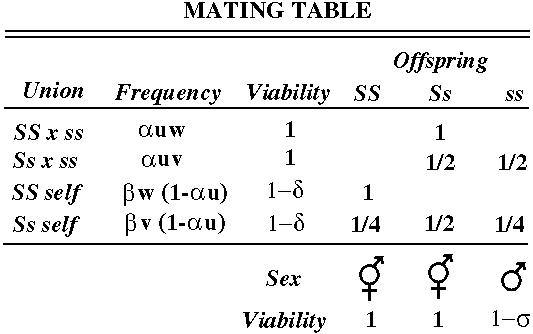
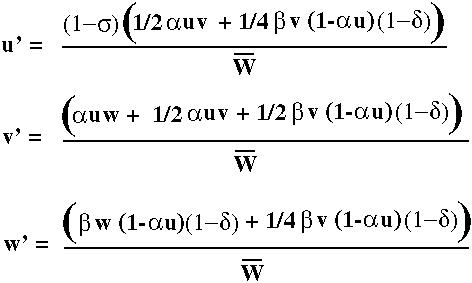
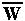Modeling this Sex Determination System

From the mating table, we can determine the frequency of the three genotypes in the next generation:

is the average fitness and equals the sum of the numerators. We must divide by the average fitness so that u', v' and w' remain frequency measures that sum to one.

Modeling this Sex Determination System

Analysis Step 1: Determine equilibria

At equilibrium u'=u, v'=v, and w'=w. This gives us three equations in three unknowns (u, v, w).

Solving these three equations indicates that there are only two biologically interesting equilibrium states.

w=1 and only SS females exist No males, No outcrossing
u= Males present

Staring at this last equation for a while indicates that (1) the sex ratio is generally not even, (2) the sex ratio is always biased towards females unless males are much more fit than females.

Analysis Step 2: Determine which equilibria are stable

The w=1 equilibrium is the only stable equilibrium when 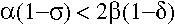. When this condition fails to hold, the population will converge towards the second equilibrium with males present.

Therefore males will be maintained in the population if they are fairly fecund (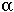 high) and fairly viable (1- 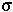high), if females are poorly able to fertilize their own eggs ( 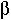low), and if there is substantial inbreeding depression (1- 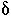low).

Notice that if there are no viability differences (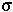 = = 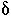0), males will only be maintained if 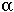> 2 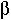. This reflects a phenomenon known as the "two-fold cost of sex".

Relating to Data

In a population from southeastern Arizona, 20% of individuals were male (ss), 60% were Ss females, and 20% were SS females.

Using these proportions, we estimate that males must have a lower fitness, being approximately 58% as viable as females. Furthermore, 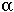must be about an order of magnitude higher than 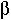(1-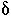) in order to be consistent with the composition of this population.

When males are encountered, most eggs must be fertilized with male sperm or most eggs must die when they are self-fertilized.

This analysis is being used by Stephen Weeks to gain further insight into the factors that allow the maintenance of sexual reproduction in this shrimp.