Methods of Analysis. II. Equilibria

• For discrete models, the equilibria are defined as those values of the variables where no changes occur from generation to generation (eg those values of p where p[t+1]=p[t]).
• For continuous models, the equilibria are defined as those values of the variables for which the rate of change equals zero (eg those values of p where dp/dt=0).

What are the equilibria of the following equations?

One-Locus Haploid Selection Model

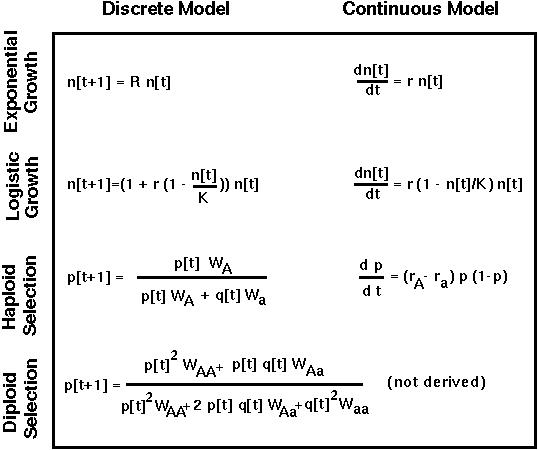
In the discrete model, we must find the value of p for which p[t+1]=p[t].

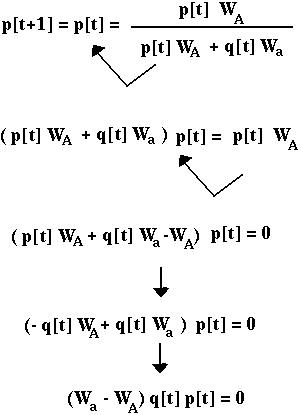
For p[t+1] to equal p[t], p[t] must equal either zero or one. The population will be at equilibrium when the population is fixed on the a or A allele. (In the special case where W_A=W_a, allele frequencies do not change regardless of p.)

Equilibrium values are often denoted by a hat; here =1 and =0 are the only equilibria.

In the continuous model, dp/dt = (r_A-r_a) p (1-p)=0 only when p or 1-p equal zero (or r_A=r_a), as in the discrete model.

One-Locus Diploid Selection Model

When p[t+1]=p[t] (i.e. the allele frequencies remain constant)

EQUILIBRIUM

To determine the equilibria for the diploid model, we must find the solution to:

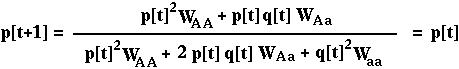
Try solving for p yourself.

If you get stuck, follow these steps:

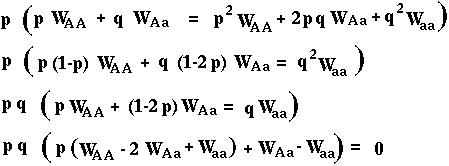
From this algebra we learn that p[t+1] will only equal p[t] in the diploid model if p=0, p=1, or

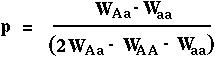
Note: Unlike the haploid genetic model, the diploid genetic model can have an equilibrium between 0 and 1. This is known as a polymorphic equilibrium.

One-Locus Diploid Selection Model

Special note: Equilibria are not always biologically valid.

Equilibria should be checked to make sure that they conform with the assumptions of the model!

For instance, in the diploid selection model, p stands for the frequency of the A allele and hence MUST fall between zero and one.

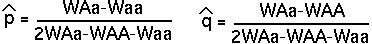
When does the polymorphic equilibrium lie between 0 and 1?

Notice that the denominator is the sum of the numerators in and .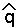

If the denominator is positive, then the numerators must both be positive for and 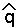to be greater than zero.

If the denominator is negative, then the numerators must both be negative for and 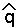to be greater than zero.

This implies that there are only two cases in which the polymorphic equilibrium is valid:

• W_Aa > W_aa and W_Aa > W_AA

• W_Aa < W_aa and W_Aa < W_AA

Examples:

• W_AA = 1, W_Aa = 1/2, W_aa = 1/4: =?

• W_AA = 1/4, W_Aa = 1/2, W_aa = 1: =?

• W_AA = 1, W_Aa = 1/4, W_aa = 1/2: =?

• W_AA = 1/2, W_Aa = 1, W_aa = 1/4: =?

Methods of Analysis. II. Equilibria

The equilibria for the other models are:

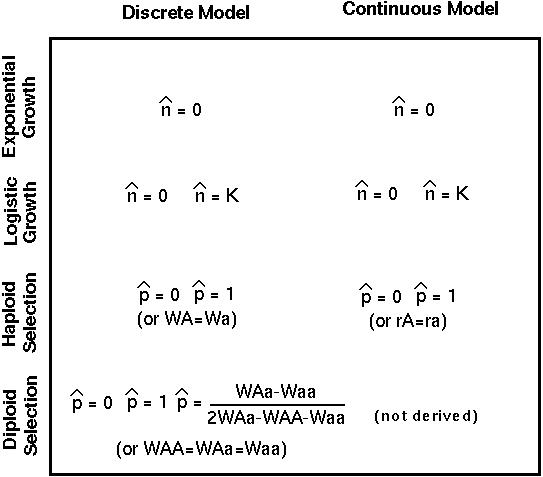
Note: Unlike the haploid genetic model, the diploid genetic model can have an equilibrium between 0 and 1. This is known as a polymorphic equilibrium.

(Make sure that you understand how to determine equilibria and can derive each of above equilibria.)

Back to biology 301 home page.