Continuous Probability Distributions

The distributions discussed so far have only a discrete set of possible outcomes (eg 0,1,2,...). Today, we'll discuss several common continuous distributions, whose outcomes lie along the real line.

One interesting point about continuous probability distributions is that, because an infinite number of points lie on the real line, the probability of observing any particular point is effectively zero.

Continuous distributions are described by probability density functions, f(x), which give the probability that an observation falls near a point x:

P(observation lies within dx of x) = f(x) dx

One can therefore find the probability that a random variable X will fall between two values by integrating f(x) over the interval:

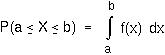
The total integral over the real line must equal one:

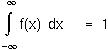
As in the discrete case, E[X] may be found by integrating the product of x and the probability density function over all possible values of x:

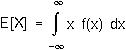
The Var(X) equals E[X2] - (E[X])2, where the expectation of X2 is given by:

Continuous Probability Distributions

Uniform Distribution

This is the simplest of continuous distributions. The probability density function is f(x)=1/(b-a) if x lies between a and b and zero otherwise:

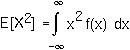
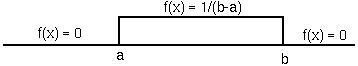
The expected value of the uniform distribution equals:

It's variance equals:

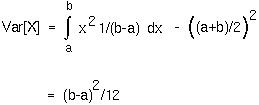
Example: Say that a particular chromosome is mapped out to be 2 morgans long. This chromosome is observed in several meiotic cells. Among those chromosomes containing a single cross-over, the mean position of the cross-over is 1 morgan from an end, but the variance is 1/2. Is this variance higher or lower than expected? What might cause such an observation?

Continuous Probability Distributions

Normal Distribution

This is the most familiar of continuous distributions. The probability density function of the normal distribution is given by:

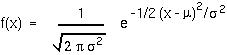
Where 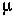is the mean and 2 is the variance of the distribution. (The mean, for example, may be found by integrating x f(x) over all values of x.)

Continuous Probability Distributions

The normal distribution arises repeatedly in biology.

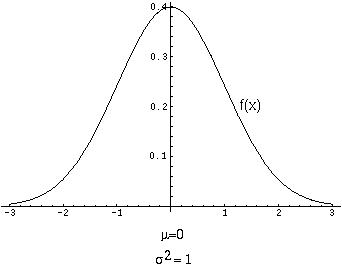
Gauss and Laplace noticed that measurement errors tend to follow a normal distribution.

Quetelet and Galton observed that the normal distribution fits data on the heights and weights of human and animal populations. This holds true for many other characters as well.

Why does the normal distribution play such a ubiquitous role?

The Central Limit Theorem For independent and identically distributed random variables, their sum (or their average) tends towards a normal distribution as the number of events summed (or averaged) goes to infinity.

For example, as n increases in the binomial distribution, the sum of outcomes approaches a normal distribution:

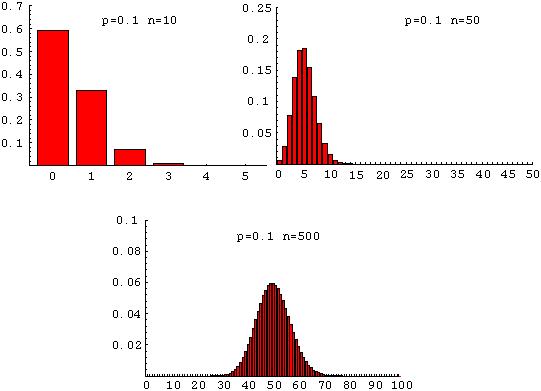
In particular, we expect that if several genes contribute to a trait, the trait should have a normal distribution. [The random variable that is being summed or averaged is the contribution of each gene to the trait.]

Continuous Probability Distributions

Exponential Distribution

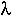If events occur randomly over time at a rate , then the time until the first event occurs has an exponential distribution:

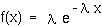
This is the equivalent of the geometric distribution for events that occur continuously over time.

E[X] can be found be integrating x f(x) from 0 to infinity, leading to the result that E[X] = 1/.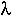

The variance of the exponential distribution is 1/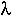2.

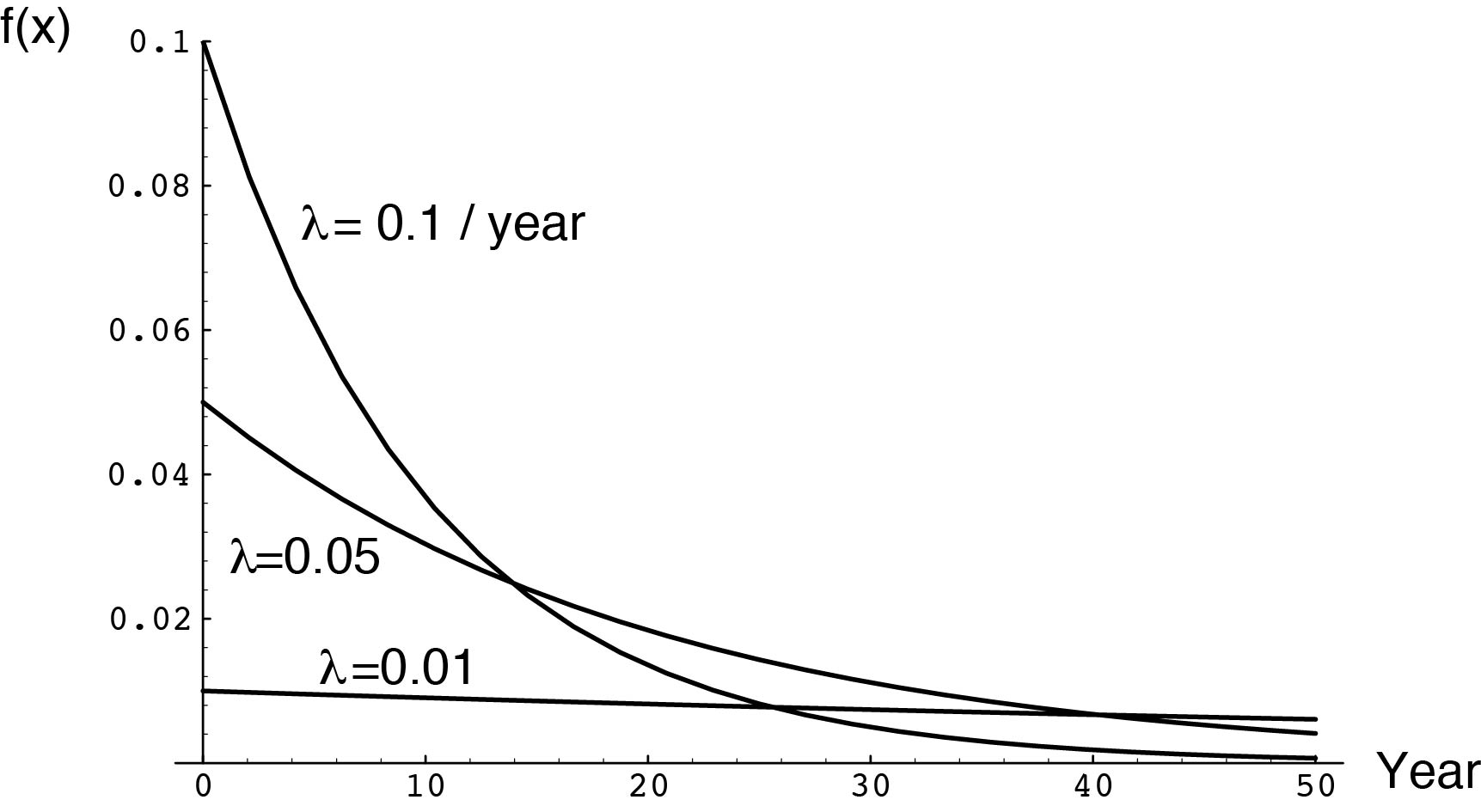
For example, let 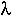equal the instantaneous death rate of an individual. The lifespan of the individual would be described by an exponential distribution (assuming that 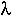does not change over time).

Continuous Probability Distributions

Gamma Distribution

As the negative binomial generalizes the geometric distribution, the gamma distribution generalizes the exponential distribution. It describes the waiting time until the rth event for a process that occurs randomly over time at a rate :

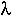The mean of the gamma distribution is r/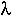 and the variance is r/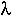2.

Example: If, in a PCR reaction, DNA polymerase synthesises new DNA strands at a rate of 1 per millisecond, how long until 1000 new DNA strands are produced? (Assume that DNA synthesis does not deplete the pool of primers or nucleotides in the chamber, so that each event is independent of other events in the PCR chamber.)

Continuous Probability Distributions

Example: If you are studying lion hunts and observe 1 successful hunt every second day on average, how long will it take for you to collect 100 data points? If your committee asks you to give an upper 95% confidence limit on how long it would take for you to complete your data collection, how might you answer them?

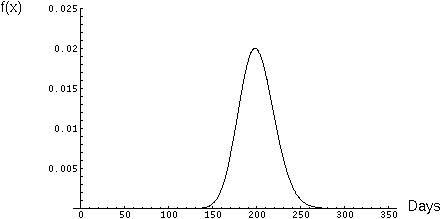
You could answer them by integrating the gamma distribution from 0 up until 95% of the area under the curve is covered. The answer in this case would be 234 days.

Or you could answer them by saying that because of the Central Limit Theorem, the distribution of the number of days should be approximately normal with mean r/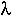 and variance r/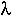2.

By using a statistical table, you figure out that the upper 95% confidence limit is 1.65 standard deviations above the mean. In this case, your estimate would be 200 + 1.65*Sqrt(400) = 233 days. (Pretty good!)

Either way, you tell your committee not too worry, it shouldn't take you much longer than 200 days to collect your data.

Back to biology 301 home page.