
Probabilistic Model: An Example from Population Genetics



Haldane (1927) used a probabilistic model to estimate the probability (P) that a new beneficial mutation would fix within a population. This provides an interesting example of the use of probabilistic modeling in biology.
The model was based on the assumptions that there will roughly be one child per parent, on average, in a population of constant size and that the distribution of the number of offspring can be described by a Poisson distribution:
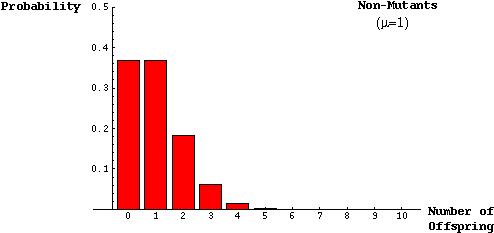


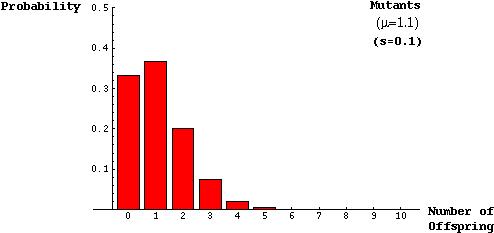
The probability that a mutant parent will have k mutant offspring is (from the Poisson):
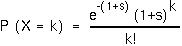
Haldane's method relied upon the insight that for a new mutation to be lost eventually, it must either not be passed on to any offspring or passed on to offspring who, in the long term, fail to leave descendents.
But the probability that each offspring will fail to leave descendants is defined as 1-P. That is, P, the fixation probability, can be interpretted as the probability that a mutation will, in the long run, have descendants in the population.


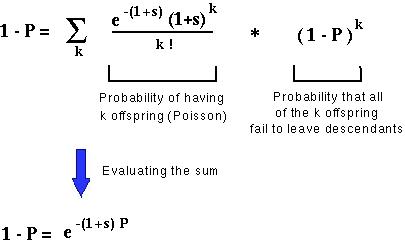
This equation can be solved numerically for P, the fixation probability.
Alternatively, one can show that if s is small, P will be small and so a Taylor Series of the above equation shows that, to leading order in s, the fixation probability of an allele is 2s.
This indicates that a substantial amount of chance is involved in the spread and fixation of a beneficial allele. Even a mutation that confers a 10% advantage to its carriers has only a 20% chance of establishing itself within a population.