Applications of the Theory
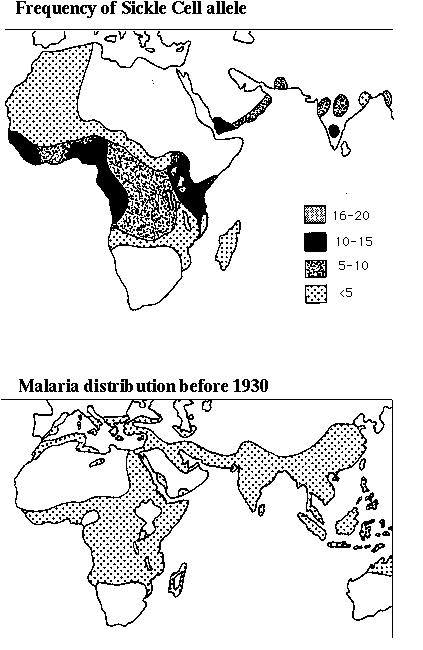
The sickle cell allele (S) of the gene for hemoglobin causes red blood cells to collapse.
In areas with a high incidence of malaria, heterozygous carriers of the sickle cell allele become more frequent with age, suggesting that selection favors them.
"The ratio of the frequency of the sickle-cell trait carriers among newborns to that among reproducing adults should, in fact, supply a direct estimate of the fitness of the normal homozygote relative to that of the heterozygote."Cavalli-Sforza & Bodmer (1971) The Genetics of Human Populations.
WAA=0.85 WAS=1
Individuals who are homozygous for sickle cell (SS) are subject to episodes of severe anemia and tend to die at an early age (WSS is near 0).
In areas where malaria is common, what is the expected frequency of the sickle cell allele?
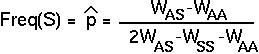
In an area where the incidence of malaria is only 1/3 as common, what is the expected frequency of the sickle cell allele?
These estimates are in keeping with the observed distribution of the sickle cell allele:
How long would it take for a population to reach equilibrium in the presence of malaria if the sickle-cell allele is initially at a frequency of 1 in a million?
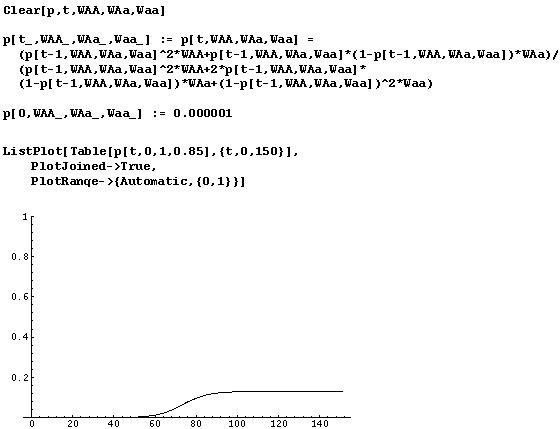
It would roughly take 100 generations to reach equilibrium, which for humans corresponds to approximately 2000 years.
It is thought that incidence of malaria increased dramatically with the development of agriculture, as forests were cleared and people concentrated in villages. This occured in West Africa at approximately 2000 BC, indicating that the sickle cell allele has probably been at near equilibrium levels for quite some time.
If malaria were eradicated, how long would it take for the sickle-cell allele to drop back down from a frequency of 0.13 to a frequency of one in a thousand, assuming that heterozygotes are as fit as non-sickle cell individuals?
For humans, this corresponds to nearly 20,000 years, indicating that selection acting only against the SS genotype is fairly inefficient.
How long would it take if carriers of sickle-cell (AS) had a slight selective disadvantage in the absence of malaria (say WAS=0.99)?
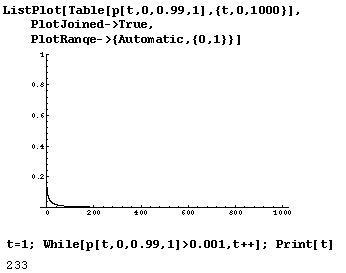
This corresponds to 4600 years, indicating that selection would be much more efficient at eliminating the sickle-cell allele if carriers are less fit.
The mean RELATIVE fitness of a population is calculated as the frequency of each type in the population times its fitness. For the haploid viability model in discrete time:
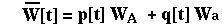
The variance in relative fitness would be:
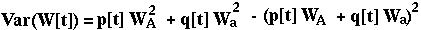
Is W[t+1] always greater than or equal to W[t]? First, note that:
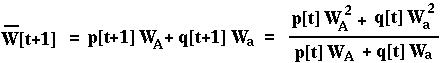
From this,
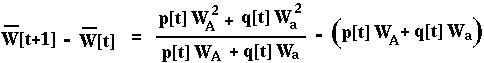
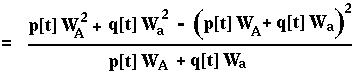
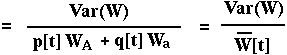
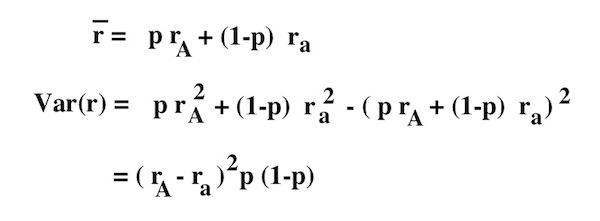
Using the chain rule:
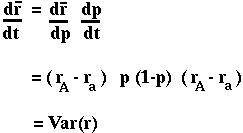
In both cases, the mean fitness changes each generation in proportion to the variance in fitness. Since a variance can never be negative, the mean fitness must increase or stay the same over time.
Fundamental Theorem of Natural Selection.
"The rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time."-- Fisher (1930) The Genetical Theory of Natural Selection
Remark 2: Variance in fitness will be highest (and mean fitness increases greatest) when p(1-p) is high, which occurs when gene frequencies are near 1/2.
Problem: While mean RELATIVE fitness may increase over time, this does not mean that the mean ABSOLUTE fitness of the population is increasing.
In fact, as Fisher (1930) noted, the mean absolute fitness of a population cannot increase indefinitely since the world would soon become overrun with a species that was growing exponentially.
He argued, that in the long-term, the mean absolute fitness of a population must hover around one (one offspring per parent). This was achieved, in his view, by a balance between the "progress" of natural selection and a "deterioration" of the environment:
"Against the rate of progress in fitness must be set off, if the organism is, properly speaking, highly adapted to its place in nature, deterioration due to undirected changes either in the organism [mutations], or in its environment [geological, climatological, or organic]."-- Fisher (1930) The Genetical Theory of Natural Selection
Populations were kept in a chemostat (a fairly constant environment) at a population size of about 5 billion.
Initially, the population was started from a single clone (one genotype).
A neutral marker, canavanine resistance then increased in frequency due to mutation pressure alone (amino acid mutation rate = 10-7), although the mutations always remained low in frequency (< 10-5) during the hundreds of generations of the experiment.
When a beneficial mutation occurred, it was most likely to arise in a canavanine sensitive cell.
The beneficial mutation would then sweep through the population. Canavanine sensitivity would "hitch-hike" along, driving back down the frequency of canavanine resistance.
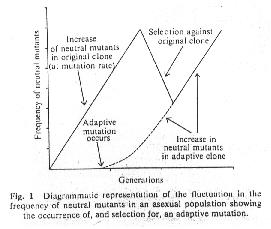
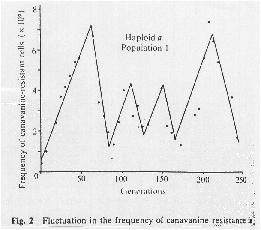
Clones isolated at various generations were then pulled from the population and competed against one another to determine relative fitness:
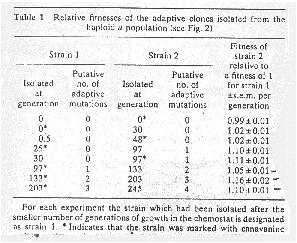
Overall, putative adaptive sweeps were observed at a rate of 3.6 10-12 per haploid cell per generation and 5.7 10-12 per diploid cell per generation.
In their experiments, this corresponds to one putative adaptive sweep every 57 generations for the haploid populations and every 39 generations for the diploid ones.
"Adaptive mutations are shown to have a higher frequency of fixation in evolving diploid than in evolving haploid populations of the yeast Saccharomyces cerevisiae, providing direct evidence that it may be an evolutionary advantage to be diploid." (Paquin & Adams 1983)
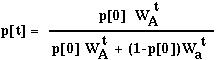
where
For the allele to be present in 90% of the population would take:
Even to reach a frequency of 10% would take 212 generations.
Similarly the spread of the allele in the diploid population would take hundreds of generations starting from such a low frequency.
This calls into question the claim that the adaptive mutations are spreading to fixation and that new adaptive mutations occur within previous adapted lines.
"Population turnovers every 37 generations are too fast... This implies that advantageous mutations will not be selected sequentially, i.e. the population from the third turnover will not contain the mutation selected in the second.[A further experiment by Adams et al (1985)] provides additional evidence that an adaptive strain is not always derived from the previous one. For example, adaptive strain 3 in the haploid cells could have an advantage over strain 2 because of a released toxin and strain 4 could be a derivative of 2 which is resistant to this toxin."
Dykhuizen (1990) Experimental Studies of Natural Selection in Bacteria
We therefore cannot yet tell whether the haploid or the diploid strain had a higher frequency of fixation of adaptive mutations.
These conclusions come directly from applying the population genetic model of selection to the experimental results.
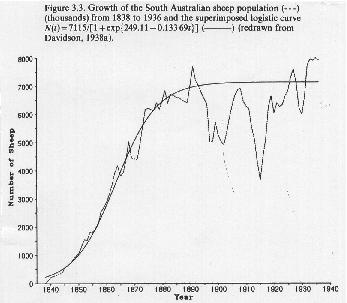
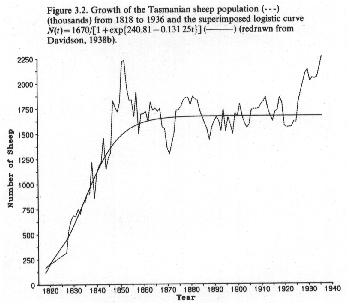
Human populations have been increasing at a nearly exponential rate over the last couple of thousand of years. Clearly, there must be an upper limit to such growth, but the carrying capacity of the earth for humans is not known.
In the 1940's several authors including Hartley (1943) and Pearl (1940) used the logistic equation to project the size of the human population over the next few decades.
Not knowing the value of K, they could not transform the data in order to estimate r using a linear regression.
Instead, they performed a non-linear regression analysis to determine both r and K simultaneously.
Here are the data and fitted curves from Hartley (1943):
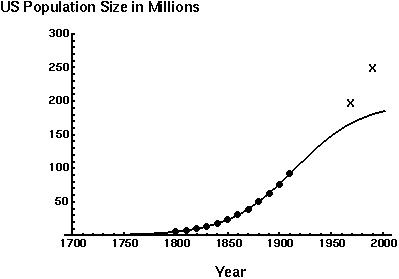
These projections fall short of the recent estimates of the US population size, which exceed the estimated carrying capacity of the US (197 million).
One likely explanation is that agricultural and technological advances have led to an increased carrying capacity, extending the growth phase of the human population.
Back to biology 301 home page.